En coordenadas cartesianas
Forma cartesiana centrada en origen
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de las abscisas y b al eje de las ordenadas la elipse es horizontal, si es al revés, entonces es vertical. El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el semieje mayor.
Forma cartesiana centrada fuera del origen
Si el centro de la elipse se encuentra en el punto (h,k), la ecuación es:
En coordenadas polares
Forma polar centrada en origen
En coordenadas polares, con origen en su centro, la ecuación de la elipse es:
(epc 1)
Una ecuación más elegante que la anterior (pero que obliga a pre-calcular la excentricidad  ), es:
), es:
 ), es:
), es:(epc 2)
Para ambas ecuaciones a es el semieje mayor, b es el semieje menor de la elipse, θ es el ángulo polar y para la () ε es la excentricidad.
Si no se quiere pre-calcular la excentricidad  convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().Formas polares centradas en un foco
En coordenadas polares, con el origen en uno de sus focos, la ecuación de la elipse es:
(501)
Para el otro foco:
(502)
En el caso un poco más general de una elipse con un foco en el origen y el otro foco en la coordenada angular  , la forma polar es:
, la forma polar es:
 , la forma polar es:
, la forma polar es:(503)
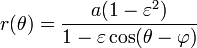 }
}El ángulo
 de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas
de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas  es el llamado semi-latus rectum de la elipse, normalmente denotado
es el llamado semi-latus rectum de la elipse, normalmente denotado  . El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
. El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.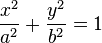





No hay comentarios:
Publicar un comentario